SEMINARIO DE ESTADÍSTICA APLICADA A LA EDUCACIÓN: XV. ESTADÍSTICA NO PARAMÉTRICA

ESTADÍSTICA NO PARAMÉTRICA

La estadística no paramétrica es una rama de la estadística que estudia las pruebas y modelos estadísticos cuya distribución subyacente no se ajusta a los llamados criterios paramétricos. Su distribución no puede ser definida a priori, pues son los datos observados los que la determinan. La utilización de estos métodos se hace recomendable cuando no se puede asumir que los datos se ajusten a una distribución conocida, cuando el nivel de medida empleado no sea, como mínimo, de intervalo.

Las principales pruebas no paramétricas son las siguientes:

PRUEBA BINOMIAL

La prueba binomial analiza variables dicotómicas y compara las frecuencias observadas en cada categoría con las que cabría esperar según una distribución binomial de parámetro especificado en la hipótesis nula.

La secuencia para realizar este contraste es:

Analizar

Pruebas no paramétricas

Binomial

PRUEBA DE RACHAS

El contraste de rachas permite verificar la hipótesis nula de que la muestra es aleatoria, es decir, si las sucesivas observaciones son independientes. Este contraste se basa en el número de rachas que presenta una muestra. Una racha se define como una secuencia de valores muestrales con una característica común precedida y seguida por valores que no presentan esa característica. Así, se considera una racha la secuencia de k valores consecutivos superiores o iguales a la media muestral (o a la mediana o a la moda, o a cualquier otro valor de corte) siempre que estén precedidos y seguidos por valores inferiores a la media muestral (o a la mediana o a la moda, o a cualquier otro valor de corte).

Si la muestra es suficientemente grande y la hipótesis de aleatoriedad es cierta, la distribución muestral del número de rachas, R, puede aproximarse mediante una distribución normal de parámetros:

donde n1 es el número de elementos de una clase, n2 es el número de elementos de la otra clase y n es el número total de observaciones.

LA PRUEBA DE LA MEDIANA.

La prueba de la mediana es una prueba no paramétrica que podemos considerar un caso especial de la prueba de chi-cuadrado, pues se basa en esta última. Su objetivo es comparar las medianas de dos muestras y determinar si pertenecen a la misma población o no.

Para ello, se calcula la mediana de todos los datos conjuntamente. Después, se divide cada muestra en dos subgrupos: uno para aquellos datos que se sitúen por encima de la mediana y otro para los que se sitúen por debajo. La prueba de chi-cuadrado determinará si las frecuencias observadas en cada grupo difieren de las esperadas con respecto a una distribución de frecuencias que combine ambas muestras.

LA PRUEBA DE LOS SIGNOS

La prueba de los signos de Wilcoxon es una prueba no paramétrica para comparar la mediana de dos muestras relacionadas y determinar si existen diferencias entre ellas. Se utiliza como alternativa a la prueba t de Student cuando no se puede suponer la normalidad de dichas muestras. Debe su nombre a Frank Wilcoxon, que la publicó en 1945.^[]

Se utiliza cuando la variable subyacente es continua pero presupone ningún tipo de distribución particular.

Planteamiento

Supóngase que se dispone de n pares de observaciones, denominadas $(x_i, y_i)$ . El objetivo del test es comprobar si puede dictaminarse que los valores $x_i$ e $y_i$ son o no iguales.

Suposiciones

Si $z_i=y_i-x_i$ , entonces los valores $z_i$ son independientes.
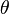Los valores $z_i$ tienen una misma distribución continua y simétrica respecto a una mediana común $\theta$ .

Método
La hipótesis nula es $H_0$ : $\theta=0$ . Retrotrayendo dicha hipótesis a los valores $x_i, y_i$ originales, ésta vendría a decir que son en cierto sentido del mismo tamaño.
Para verificar la hipótesis, en primer lugar, se ordenan los valores absolutos $|z_1|,\dots,|z_n|$ y se les asigna su rango $R_i$ . Entonces, el estadístico de la prueba de los signos de Wilcoxon, $W^+$ , es
$W^+=\sum_{z_i > 0} R_i,$
es decir, la suma de los rangos $R_i$ correspondientes a los valores positivos de $z_i$ .
La distribución del estadístico $W^+$ puede consultarse en tablas para determinar si se acepta o no la hipótesis nula.

La prueba de Mann-Whitney

En estadística la prueba U de Mann-Whitney (también llamada de Mann-Whitney-Wilcoxon, prueba de suma de rangos Wilcoxon, o prueba de Wilcoxon-Mann-Whitney) es una prueba no paramétrica aplicada a dos muestras independientes. Es, de hecho, la versión no paramétrica de la habitual prueba t de Student.

Planteamiento de la prueba

La prueba de Mann-Whitney se usa para comprobar la heterogeneidad de dos muestras ordinales. El planteamiento de partida es:

Las observaciones de ambos grupos son independientes

Las observaciones son variables ordinales o continuas.
Bajo la hipótesis nula, las distribuciones de partida de ambas distribuciones es la misma.
Bajo la hipótesis alternativa, los valores de una de las muestras tienden a exceder a los de la otra: P(X > Y) + 0.5 P(X = Y) > 0.5.

Cálculo del estadístico

Para calcular el estadístico U se asigna a cada uno de los valores de las dos muestras su rango para construir

$U_1=R_1 - {n_1(n_1+1) \over 2}$

$U_2=R_2 - {n_2(n_2+1) \over 2}$

donde n₁ y n₂ son los tamaños respectivos de cada muestra; R₁ y R₂ es la suma de los rangos de las observaciones de las muestras 1 y 2 respectivamente.

El estadístico U se define como el mínimo de U₁ y U₂.

Distribución del estadístico

La prueba calcula el llamado estadístico U, cuya distribución para muestras con más de 20 observaciones se aproxima bastante bien a la distribución normal.

La aproximación a la normal, z, cuando tenemos muestras lo suficientemente grandes viene dada por la expresión: