CONCEPTOS BÁSICOS.
Probabilidad: Es un valor numérico que representa la oportunidad o posibilidad que un evento en particular ocurra.
La probabilidad es una porción o fracción cuyo valor varia entre 0 y 1. Si un evento es imposible, tiene una probabilidad de 0, pero si el evento ocurrirá con toda seguridad, entonces tiene una probabilidad de 1.
Experimento: Proceso que conduce a que ocurra una (y solamente una) de varias observaciones posibles.
En probabilidad, un experimento tiene dos o más resultados posibles, y es incierto cual es el que ocurrirá.
Espacio muestral: Se le llama al conjunto de todos los posibles resultados individuales de un experimento aleatorio.
Evento: Conjunto de uno o más resultados de un experimento.
En el experimento de lanzar un dado existen seis resultados posibles, pero hay muchos eventos posibles.
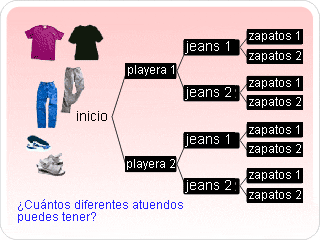Diagrama de árbol: Es el dibujo que se usa para enumerare todos los resultados posibles de una serie de experimentos en donde cada experimento puede en un número finito de maneras.
El enfoque clásico: Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:
P(A) = x
(x + z)
El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible. Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor de probabilidad antes de observar cualquier evento de muestra.
El enfoque de frecuencia relativa: También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un número de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
P(A) = x
n
|
Tanto el enfoque clásico como el enfoque empírico conducen a valores objetivos de probabilidad, en el sentido de que los valores de probabilidad indican al largo plazo la tasa relativa de ocurrencia del evento.
El enfoque subjetivo: Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal.
TIPOS DE EVENTOSEventos Independientes: Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Eventos dependientes: Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que A|B no es una fracción.
P(A|B) = P(A y B)/P(B) o P(B|A) = P(A y B)/P(A)
Reglas de Multiplicación. Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
Reglas de Multiplicación. Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(B|A) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(A|B) si A y B son dependientes
Eventos mutuamente excluyentes: Dos o más eventos son mutuamente excluyentes o disjuntos, si no pueden ocurrir simultáneamente. Es decir, la ocurrencia de un evento impide automáticamente la ocurrencia del otro evento (o eventos).
Eventos no excluyentes: Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea.
Reglas de la Adición. La Regla de la Adición expresa que: la probabilidad de ocurrencia de al menos dos sucesos A y B es igual a:
P(A o B) = P(A) U P(B) = P(A) + P(B) si A y B son mutuamente excluyente
P(A o B) = P(A) + P(B) – P(A y B) si A y B son no excluyentes
Siendo: P(A) = probabilidad de ocurrencia del evento A
P(B) = probabilidad de ocurrencia del evento B
P(A y B) = probabilidad de ocurrencia simultanea de los eventos A y B
PRINCIPIO FUNDAMENTAL DE CONTEO
Combinaciones: Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.
Para calcular el número de combinaciones se aplica la siguiente fórmula:
Cm,n = m! .
n! * (m-n) !
El término "n!" se denomina "factorial de n" y es la multiplicación de todos los números que van desde "n" hasta 1.
Permutaciones: Calcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos.
La expresión "Pm" representa las permutaciones de "m" elementos, tomando todos los elementos. Los subgrupos se diferenciaran únicamente por el orden de los elementos.
Enfoque axiomático:
Los axiomas por si mismos no requieren demostración, pero si se va a aplicar la teoría resultante, debemos demostrar que se cumplen los axiomas cuando damos a las probabilidades un significado “real”.
Axioma 1
La probabilidad de un evento es un numero real no negativo; o sea, P(A)" 0 para cualquier subconjunto de A de S.
Axioma 2
P(S) = 1
Axioma 3
Si A1, A2, A3, …, es un secuencia finita o infinita de eventos mutuamente exclusivos de S entonces
P(A1 U A2 U A3 U …)= P(A1) + P(A2) + P(A3) + …
|
Los axiomas por sí mismo no requieren demostración, pero si se va a aplicar la teoría resultante, debemos demostrar que se cumplen los axiomas cuando damos a las probabilidades un significado “real”.
Como las proporciones son siempre positivas o cero, el primero axioma coincide por completo con la interpretación de la frecuencia. El segundo axioma expresa indirectamente que la certeza se identifica con una probabilidad de 1 (después de todo, siempre se supone que debe ocurrir una de las posibilidades de S y es a este evento cierto que asignamos una probabilidad de 1. Hasta donde atañe a la interpretación de la frecuencia, una probabilidad de 1 implica que el evento en cuestión ocurrirá el 100% del tiempo o bien, dicho de otra manera, que ocurre con certeza.
Tomando el tercer axioma en el caso más simple; o sea, en relación con dos eventos mutuamente exclusivos A1 y A2, se aprecia fácilmente que se cumple a través de la interpretación de la frecuencia. Si un evento ocurre.
Probabilidad condicional:
En la práctica es común enfrentarnos al problema de obtener la probabilidad de un evento, condicionado a la ocurrencia o no ocurrencia de otro, esto es, el caso en que la ocurrencia de un evento altera las condiciones de las que depende la probabilidad del otro, estas probabilidades se llaman probabilidades condicionadas. Si A y B son los eventos en cuestión, tenemos que P(A/B) es la probabilidad de A dado que ya ocurrió el evento B. P(B/A) es la probabilidad de B dado que A ya ocurrió.
Sea E un evento maestral arbitrario de un espacio maestral S con P(E) > 0. La probabilidad de que un evento A suceda una vez que E haya sucedido, se define como:
P(A/E) = P (A∩E)
P(E)
Donde:
P (A/E) es la probabilidad de que se dé el suceso A condicionada a que se haya dado el suceso E.
P (A∩E) es la probabilidad del suceso simultáneo de A y de E.
P (E) es la probabilidad a priori del suceso E.
P (A/E) = TOTAL DE MANERAS DE A∩E
TOTAL DE MANERAS DE E
Teorema de Bayes:
P(A/B) = P (A∩
P (B)
La fórmula anterior es simplemente una forma específica de la fórmula general para la probabilidad condicional; sin embargo, la importancia especial del teorema de Bayes consiste en que se aplica en el contexto de eventos secuenciales y además, en que la versión de cálculo de la fórmula proporciona la base para determinar la probabilidad condicional de un evento que ha ocurrido en la primera posición secuencial, dado que se ha observado un evento especifico en la segunda posición secuencial. La forma de cálculo para el teorema específico de Bayes es:
P(A/B) = P(A) P(A/B) .
P(A1) P(A/B1) + P(A2) P (A/B2)4... + P(An) P(B/An)
No hay comentarios:
Publicar un comentario